Fixed Cost

View FREE Lessons!

Definition of Fixed Cost:

Fixed costs are costs that are not directly influenced by how much of a good or service is produced. Examples of fixed costs include rent, mortgage payments, telephone bills, and salaries of essential personnel.

Detailed Explanation:

Do you have expenses that you are locked into? Perhaps rent, a phone bill, or an insurance premium? These are examples of your fixed costs. Economists separate business costs into two categories: fixed and variable. Fixed costs are unaffected by output, while variable costs are directly related to output. Examples of variable costs include raw materials and wages paid to hourly workers directly involved in the production of a good or service. To distinguish between fixed and variable costs ask yourself, “Will this cost increase if more of a good or service is provided?” If the answer is “No” then the cost is fixed. However, fixed costs change over time. For example, insurance is a fixed cost, because the premium is normally not affected by the production level, but an insurance premium may change from one period to the next. Advertising is generally considered a fixed cost because it is not tied to production, but a business may choose to reduce its overhead by advertising less. In an extreme case, a business may choose to close, and thus eliminate all of its fixed costs. Most fixed costs are time-related, such as annual salaries, or monthly rent. In the long run, all fixed costs are variable.

The Fixed and Variable Costs graph below illustrates a business’s cost structure. The blue line, which represents the company's fixed costs, is horizontal because it is unaffected by output. It intersects the y-axis at the total fixed cost because fixed costs must be paid even when there is no production. In the illustrated example, the fixed cost equals $500, and the company would incur a $500 cost if production dropped to zero (such as when a manufacturing plant closes for a week in the summer), and remains at $500 if production increases to 14 units. The orange line represents the business's variable costs. Variable costs are expressed on a per-unit basis. On the graph it is assumed that the variable cost per unit remains constant, so the total variable cost (TVC) equals the variable cost per unit (VC) times the number of units produced (Q). TVC = VC (Q). The variable cost graph originates at the origin and has a positive slope equal to the variable cost per unit. The formula for total costs is fixed costs plus the total variable cost (FC + TVC), where FC is fixed costs. The total cost curve is the sum of the variable and fixed cost curves. 

 

Assume you are considering opening a small ice cream parlor. Understanding your cost structure can help you quickly estimate your profit at different outputs. After doing some research, you estimate your total monthly fixed expense would be $1,100. This includes rent, utilities, and other overhead expenses. Your variable cost would be approximately $1.20 per scoop sold. The variable cost includes tubs of ice cream, cups, napkins, and labor. You plan to price your ice cream at $2.50 per scoop. How much would you earn if you sold 5,000, 7,500 or 10,000 scoops in a month? The table below summarizes your estimates. Note that your fixed costs remain constant and your variable costs are directly related to the number of scoops sold. 



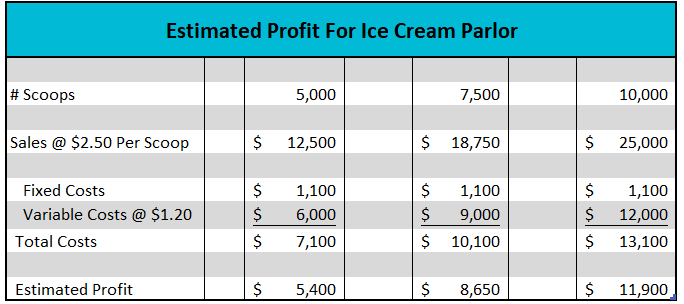
How many scoops would you need to sell to cover your fixed and variable expenses? In business, this is known as your break-even. Every scoop generates $1.30 in revenues that can be used to pay your fixed costs (Price – VC). If your fixed costs total $1,100, you would need to sell 847 scoops to cover your fixed costs or break-even. The break-even formula is:

Break-Even # Units = FC / (Price - VC)

Break-Even # Units = $1,100 / $2.50 - $1.20

Fixed costs have a direct impact on a company's break-even. If the fixed costs increases, more of a good or service would need to be produced to achieve break-even, assuming there is no change in the variable cost or price.

Dig Deeper With These Free Lessons:

Output and Profit Maximization
Fundamental Economic Assumptions
Factors of Production – The Required Inputs of Every Business
Marginal Analysis – How Decisions Are Made