A Nash equilibrium outcome (NEO) is an outcome when no player can change his or her strategy for personal gain – assuming each player’s decision remains unchanged.
Decisions are not made in isolation. People, businesses, and governments consider what they believe their “competitors” will do before reaching a decision. The late John Nash, Jr. developed the concept of a Nash equilibrium outcome. He was awarded a Nobel Prize in 1994 for his research. (Dr. Nash was portrayed by Russell Crowe in the movie A Beautiful Mind.)
Have you ever considered what another person might do when making a decision that would affect your satisfaction? After making the decision you realize that you would have made the same decision no matter what the other person chose. That decision is your dominant strategy. If the other person reached the same conclusion you would have reached an NEO. An NEO is stable because players will not change their decisions since they have nothing to gain. However, in some cases, the decision may not be the best choice for either party.
Consider the example of Wedge Inn in Hungryville in identifying an NEO. Wedge Inn is Hungryville’s only restaurant. One harsh winter, a large snowstorm knocks out power, cell, and landline phone service in most of the town. Bob, the owner of Wedge Inn, doesn’t know what his customers will do, and Hungryville’s residents have no way of knowing if Wedge Inn is open. Bob must decide to either remain open or close. Simultaneously, the residents must choose whether to visit Wedge Inn or stay home.
Bob’s best choice depends on what he believes Hungryville’s residents will do. Meanwhile, a resident’s best choice depends on Bob's decision on whether or not to open. There are four possible outcomes:
Consider the perspective of the residents. Their degree of happiness is ranked on a scale from zero to ten, where zero is very unhappy and ten is very happy. They also have four possible outcomes:
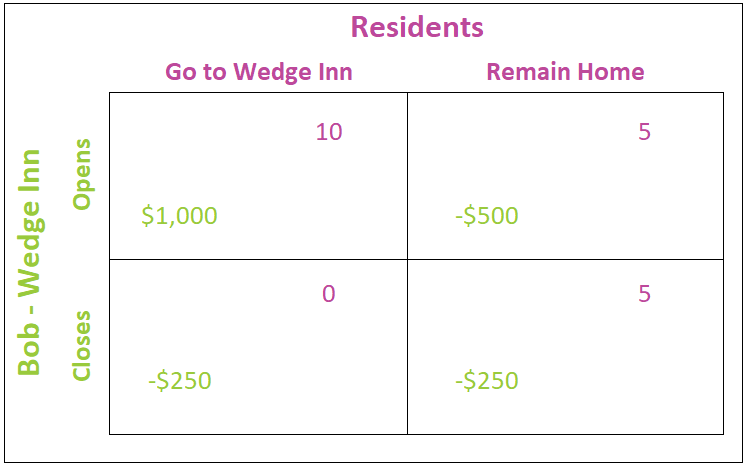
A Nash equilibrium can be identified using a payoff table. The table above displays the outcomes, (or payoffs) for each possible decision in a way that helps identify the most likely outcome. During the snowstorm, Bob’s choices are to either stay open or close. These options appear in green on the vertical axis. Hungryville’s residents have the choice either to go to Wedge Inn or to remain at home during the snowstorm. These options are shown in purple on the horizontal axis. Follow the payoff matrix as each scenario is reviewed.
Now, let’s use this payoff table to identify a Nash equilibrium outcome. When determining an NEO, it is helpful to consider each player’s perspective, and remember that each player wants to maximize his or her satisfaction. In the scenario of Wedge Inn and the Hungryville snowstorm, there are two NEOs because there are two possible endpoints where neither party would gain from changing their mind upon learning the other player’s decision. One is achieved when Wedge Inn opens and Hungryville’s residents dine there. Considering Bob’s perspective, when his customers choose Go, Bob gains the most by choosing Open because he earns $1,000 rather than losing $250 if he chooses Close. There is no incentive for Bob to change his strategy from Open to Close if his customers don’t change their strategy from Go to Remain Home.
Next, look at the customer’s perspective. Do they have any incentive to change their strategy if Bob doesn’t? If Bob chooses Open, his customers would prefer to Go to Wedge Inn and receive a high happiness score of ten rather than Remain Home and have a satisfaction of five. So, there is no incentive for Bob’s customers to change their strategy from Go to Remain Home. The combination of Open and Go is an NEO because neither Bob nor his customers would benefit from changing their choice when learning the other player’s decision.
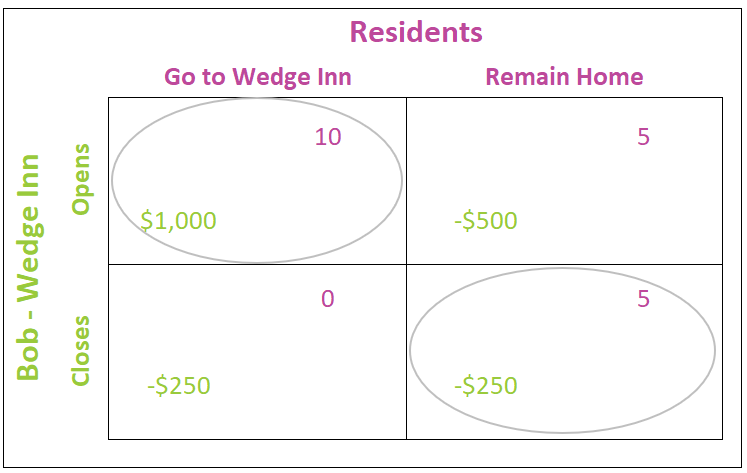
A second Nash equilibrium is reached when the residents remain home and Wedge Inn closes. In this case, neither can improve their level of satisfaction by changing their decision. If Wedge Inn is closed, the residents would experience a drop in their satisfaction from five to zero if they ventured out in the snow. Bob’s loss would increase from $250 to $500 if he had opened and the residents had remained home. The two NEOs are circled on the table below.
Most leaders agree that global warming is a problem and carbon emissions need to be reduced. Yet it has been very difficult for world leaders to reach an agreement. Identifying the Nash equilibrium outcome is useful in understanding why. Assume two neighboring countries, A and B, acknowledge that carbon emissions contribute to global warming, and ultimately will cause severe ecological problems if emissions are not reduced. However, these countries compete in the global economy. A country’s leadership does not want to lose a competitive advantage from investing in pollution abatement. Reducing carbon emissions is expensive, takes time, and causes a competitive disadvantage if one country chooses to clean up, while the other country continues to pollute.
The table below is a payoff matrix for the possible outcomes when countries A and B choose between reducing or not reducing their carbon emissions. Payoffs include the environmental benefits and negative payoffs such as the environmental damage and the cost of reducing carbon emissions. These costs include the equipment and lost income resulting from a competitive disadvantage over a country that chooses to not reduce its emissions. Society would benefit if both countries cooperate and reduce their carbon footprints, but both countries would incur enormous costs.
Assume a group of independent experts measure the tangible and intangible costs and benefits and assign a payoff to each country in every scenario. For example, the experts give each country a payoff of two when both countries reduce carbon emissions. This outcome is represented by the upper left box. Now assume Country A pollutes while B invests in reducing carbon emissions. Country A reaps the benefit of a cleaner environment resulting from Country B’s efforts while avoiding the cost of emission reduction. The experts give Country A a payoff of three. Country B is given a payoff of zero because it benefits from a partial reduction in pollution, but also incurs the high cleanup cost which makes it more difficult for B’s companies to compete in a global economy. The payoffs of A and B are reversed when B does not reduce its carbon emissions and A does. These scenarios are seen in the upper right and lower left boxes. Finally, a payoff of one has been given to each country if both choose not to reduce emissions. This is represented by the lower right box.
Is there a Nash equilibrium outcome? First, consider Country B’s payoffs if its leadership believes Country A will reduce its carbon emissions. These purple payoffs are seen in the upper row. Three is greater than two, so the leadership of Country B would choose to continue polluting. (Three has been underlined in the table below to indicate it is a dominant strategy.) What if Country B's leadership believes Country A will not reduce its emissions. This possibility is seen on the bottom row. Again, Country B would choose not to reduce its emissions because one is better than zero. The one is underlined in purple.
Country A’s perspective is similar to Country B’s. Its dominant strategies are underlined in green. If Country A’s leadership believes Country B will invest in abatement, then its payoffs are listed in the first column. Country A will not reduce its emissions because three is preferable to two. Likewise, A’s leadership will not reduce its carbon emissions if it believes Country B will do the same. In this case, a payoff of one is preferred to zero. Not reducing carbon emissions is a Nash equilibrium outcome because neither country would benefit from changing its behavior if the other does not. The NEO is circled in the table below.
In this case, the Nash equilibrium outcome is not the socially optimal outcome. Society would be better off if the countries cooperated, but countries choose to pollute because they fear the impact on their economy. Countries have been hesitant to reduce emissions without a global agreement and the ability to verify that countries that sign an agreement adhere to the terms. Using game theory to identify the Nash equilibrium outcome is helpful in understanding the challenges our leaders face when negotiating global agreements.
Game Theory
Market Structures II – Monopolistic Competition and Oligopoly