Principal
View FREE Lessons!
Definition of Principal:
Principal means of primary importance. In finance, it refers to the amount borrowed or the balance owed on a loan that has not been paid off. The principal may also refer to the key individuals such as a majority owner of a business or the decision-maker who bears the primary responsibility.
Detailed Explanation:
A bond's principal is its face value and not its market value. For example, an investor may pay $11,000 for a bond with a face value of $10,000 that pays $400 in interest annually. The principal equals $10,000 because that is the amount the investor will be paid back when the bond matures. Why would an investor pay $11,000 when the principal she will eventually be paid back is only $10,000? The answer is that the interest income more than makes up for the $1,000 loss in principal. For example, let us compare two bonds. Assume each matures in 15 years, but one pays $400, while the other pays $300 in interest annually. The bond paying $400 per year pays a total of $6,000 over the 15 years, while the bond paying $300 per year pays a total of $4,500. Some investors may prefer "losing" $1,000 when the principal is paid back in return for gaining $500 in total interest income.
When banks issue businesses or consumers a loan, the amount owed is referred to as the principal balance. A $100,000 loan would have a principal balance of $100,000 on the day the loan was originated, but the principal balance would decrease following the first payment, assuming the payment exceeded the accrued interest. Interest is calculated by multiplying the interest rate by the principal balance.
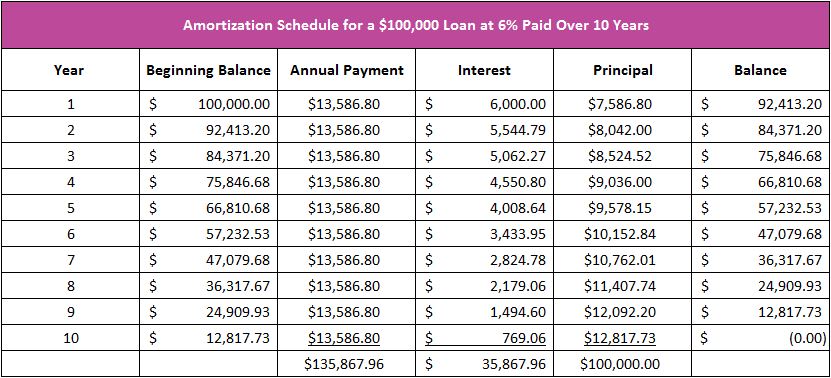
The Amortization Schedule
A loan’s amortization schedule provides a payment's allocation to interest and principal. It is helpful in understanding how debt works. When a payment is made, the interest is paid first. Interest is the price for the use of money, and it is directly related to the principal balance and the interest rate, so the larger the loan balance or the higher the interest rate, the greater the interest expense.
The table below is the amortization schedule for a $100,000 loan with an interest rate of six percent that is paid over a 10 year period. A $13,586.80 payment is due annually. During the first year, $6,000 in interest is paid (.06 x $100,000). The principal portion of the payment is derived from subtracting the interest from the payment. In our example, the reduction of principal after the first payment equals $7,586.80, or the difference between the $13,586.80 payment and $6,000 in interest. The loan balance at the end of the first year is $92,413.20, which equals $100,000 (the beginning balance), less $7,586.80 (the principal paid). The amortization schedule below shows that more interest is paid in the early stages of a loan. This is because interest is paid on the outstanding balance, and the loan balance has decreased in the second year. In the second year, the interest portion of the payment equals $5,544.80 ($92,413.20 x .06), which means that $8,042 is paid to principal ($13,586.80 - $5,544.80).
Dig Deeper With These Free Lessons:
Capital – Financing Business Growth
Entrepreneurs – Their Vital Role in the Economy
Understand a Stock’s Performance Using Supply and Demand
