Sequential Move Games
View FREE Lessons!
Definition of Sequential Move Game:
A
sequential move game is used in game theory to predict the outcome following a chain of events involving at least two parties who make decisions that impact the satisfaction of the other parties.
Detailed Explanation:
When you respond to a competitor’s decision, you are playing a sequential move game. People, businesses, and governments frequently react to moves made by others. In a sequential move game, one player makes the first decision and the second player responds. Decision trees are built where the branches represent possible decisions in the game. Several real-life examples include when companies respond to a competitor’s action, negotiations where one party makes a proposal and the second party counters, in war, when an army must determine how to defend against an attack, and how a person will respond when insulted.
Sequential move games continue for as long as players respond to another player’s move. In contrast, simultaneous games have a short time frame. Players make one move at approximately the same time and base their move on what they
expect the other players to do.
To illustrate a sequential game, consider the small town, Hungryville, where there is only one restaurant, Bob's Diner. Bob’s current yearly profit is $100,000. Suppose Kathy just moved to Hungryville and is considering opening a restaurant — Kathy’s Deli. Presently, Bob has a monopoly because he owns the only restaurant in town, which enables him to charge higher prices. But if Kathy opens a restaurant she and Bob would control Hungryville's restaurant market. Bob would lose market share, suffer a drop in his income, and most likely be forced to lower his prices. Bob has two options: he can either cooperate with Kathy knowing he will lose market share or initiate a price war by dramatically lowering his prices and retain his market share by forcing Kathy’s Deli out of business. If Kathy decides not to open a restaurant, then the game is over and nothing has changed.
 Image from iStock
Image from iStock
Decision trees help in understanding sequential move games. Follow the decision tree below to visualize the chain of possible events. Decision trees begin with an initial decision, called an “initial node,” which is depicted by an open circle. The lines emanating from the initial node represent the possible strategies the first player has. In our example, Kathy moves first. She can either enter Hungryville’s restaurant market by opening Kathy’s Deli or stay out of the market. If Kathy chooses to open, Bob must choose to either fight Kathy by lowering his prices to retain his market share or accommodate Kathy by doing nothing, with the understanding he will lose some of his business. Each point at which a player must make a choice is called a “decision node.” In the decision tree, Kathy’s decision node is an initial node which is outlined in blue. Bob’s decision node is in green.
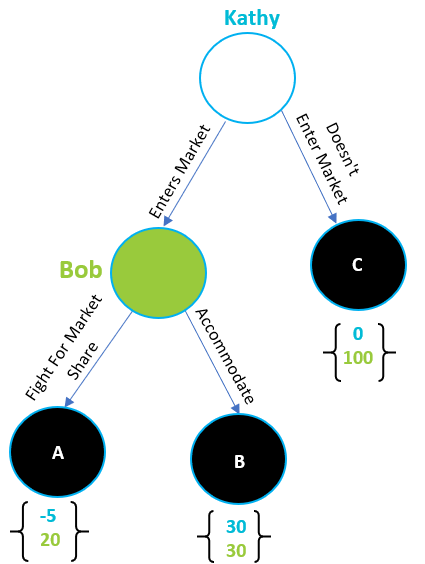
Finally, there are “terminal nodes.” The game ends when a terminal node is reached. In the decision tree, the terminal nodes are black. Once a terminal node is reached, the payoff for both players is provided. Kathy’s payoffs are in blue and Bob’s payoffs are in green. There are multiple payoffs that depend on the strategies the players employ. In our game, there are three terminal nodes, representing the three possible outcomes:
- Kathy chooses not to enter the market,
- Kathy enters the market, and Bob chooses to accommodate, and
- Kathy enters the market and Bob chooses to fight.
Payoffs for each scenario must be assumed. If Kathy decides not to open a restaurant, she doesn’t earn a profit and the game ends at terminal node C, where her payoff is zero. In this case, Hungryville’s restaurant industry is unchanged and Bob’s payoff continues to equal $100,000. What are the payoffs if Kathy opens Kathy's Deli? Bob may decide to accommodate Kathy, in which case they end up at terminal node B where they split the profit evenly. Each restaurant earns $30,000. (Bob's profit would be less than $50,000 because his fixed costs would remain unchanged and he would serve fewer people, resulting in an increase in his average cost per meal.) Finally, if Bob decides to begin a price war and fight Kathy, they end up at terminal node A. In this case, assume Bob lowers his prices enough to retain most of Hungryville’s customers, resulting in a lower profit margin, and only a $20,000 profit. Assume in this scenario that Kathy would lose $5,000. How do Kathy and Bob proceed?.
Solving Sequential Move Games Using Backwards Induction
What do people who are dating, businessmen, politicians, and military leaders have in common? Each player would like to know what the other players will do before they reach a decision. Will he like my dress? How will my competitors respond if I open a business in another county? Will my constituents approve of my decision and vote for me? How will the enemy respond to an attack? Sequential move games begin at an endpoint, specifically the best end outcome. Knowing the most probable future outcome makes it easier to make the best decision today. To identify the most likely outcome or Nash equilibrium outcome (NEO), in sequential move games, economists employ “backwards induction.” This method identifies the NEO by first determining what the best payoff is for the last player at each of the terminal decision nodes. If one payoff is better than the others, it is assumed that the strategy that achieves that outcome is chosen by the player if the game reaches that decision node. Then, determine what the best payoff is for the player who chooses at the second-to-last decision node given the last player’s strategy. Follow this process all the way up the tree, to identify the first player’s decision. This process can be used to predict Kathy's and Bob's decisions.
Begin backwards induction by looking at the payoffs associated with the last decision node. In this case, that is Bob’s decision node. Bob has two strategies: accommodate or fight. If Bob accommodates Kathy, his payoff (in green) is $30,000. If he fights Kathy, his payoff is $20,000. Bob will always prefer $30,000 to $20,000, so if he finds himself choosing between fighting and accommodating, Bob will choose to accommodate because he would prefer earning $30,000 to $20,000. To signify this strategy, a wider arrow has been placed along the “Accommodate” branch of the tree.

What are Kathy’s options? Kathy knows that if she chooses to not enter the market, her payoff is zero. But what if she chooses to enter the market? It is a tough choice because Kathy doesn’t know if Bob is going to fight or accommodate her. If Bob chooses to fight Kathy, then she will lose all her start-up costs and she will not earn a large enough profit to remain in business. However, earlier we concluded that if Bob finds himself choosing between fighting and accommodating, he will choose to accommodate. Believing Bob will accommodate her, Kathy will choose to open Kathy's Deli because she prefers $30,000 to $0. The wider blue arrow along the “Enter Market” line depicts this choice. Follow the wider arrows to identify the most likely chain of events. Kathy enters the market, Bob accommodates her, and both players earn $30,000.
Dig Deeper With These Free Lessons:
Game Theory
Market Structures Part II – Monopolistic Competition and Oligopoly
Market Structures Part I – Perfect Competition and Monopoly


