Simultaneous Move Game
View FREE Lessons!
Definition of a Simultaneous Move Game:
A
simultaneous move game is a type of game in game theory where the players choose a strategy at approximately the same time without knowing the strategy chosen by any of the other players. A simultaneous move game is also referred to as a simultaneous game.
Detailed Explanation:
Simultaneous move games are used to explain how a rational decision can result in a less than optimal outcome when one party’s decision impacts another person’s satisfaction. Rock-paper-scissors is a popular simultaneous game. In the game, two players play either rock, paper, or scissors simultaneously. The winner depends on what the other player plays. If one plays rock and the other plays scissors, rock wins because rock crushes scissors. If one player has a reason to believe their opponent will play rock, then she will play paper, because paper beats rock. In all simultaneous games, players consider their payoff based on what they expect the other player to do. Players have only one chance to make the right decision.
A payoff matrix is used to determine the most likely outcome in a simultaneous game. It includes the players, strategies, and the payoff for each player and strategy. The prisoner’s dilemma is the most used illustration of a simultaneous game and is applicable to many real-life scenarios.
 Image from iStock
Image from iStock
Suppose Alan and Barry committed two crimes. The police have enough evidence for one, but not enough to proceed with the second more serious crime. Obviously, Alan and Barry want to minimize their time in prison. In the classic prisoner’s dilemma example there are two criminals who are questioned separately by the police. The interrogator’s strategy is to get them to confess to the second crime by negotiating a plea bargain. Each prisoner is offered a lighter sentence if he confesses. Remember the prisoners are interrogated separately and do not know what the other will do, so they must independently decide whether to deny or confess to committing the crimes. The four possible outcomes are:
- Alan and Barry do not confess to committing the second crime.
- Alan and Barry confess to committing the second crime.
- Alan confesses and Barry denies committing the second crime.
- Barry confesses and Alan denies committing the second crime.
Table 1 is a payoff table that helps in understanding the possible outcomes and identifying each prisoner’s most probable decision. Payoffs (years in jail) representing Alan’s decisions are purple, and Barry’s decisions are green. In our example, Alan and Barry would not be charged with the second crime if they both deny involvement in it. Each would be sentenced to four years in prison for the first crime. This combination is seen in the bottom right box in Table 1. They would serve six years if both confess to committing the second crime (upper left box). The third and fourth possibilities are very similar. In one case Alan confesses and Barry denies involvement (bottom left box), and in the other case Barry confesses and Alan denies involvement (upper right box). In each scenario, the confessing individual would receive a one-year sentence, while the individual who stubbornly refuses to cooperate would serve ten years. How much do they trust their collaborator? Would either Alan or Barry try to reduce their sentence by confessing?
Table 1
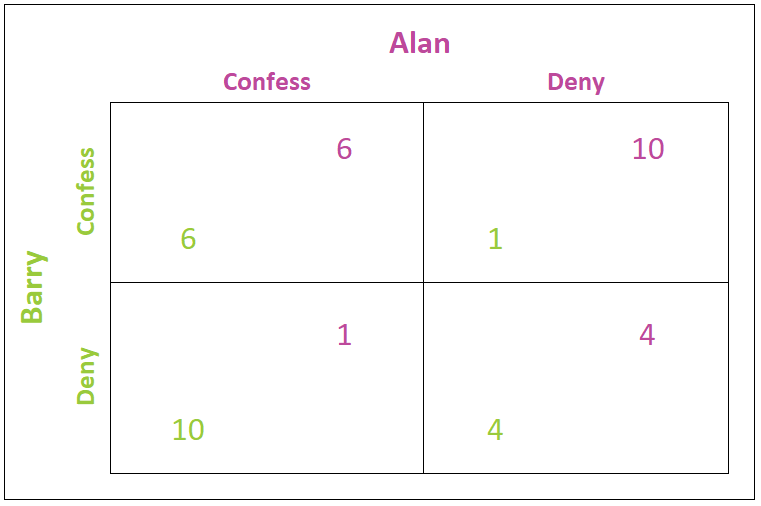
If Alan thinks Barry will confess, he will confess because he prefers six years in prison to ten. These options are in purple in the first row. Six has been underlined in Table 2 to indicate it is preferable. The second row provides the options if Alan thinks Barry will deny. Again he will confess because being incarcerated for one year is better than four. One is underlined. No matter what Barry does, it is in Alan’s best interest to confess to committing the crime. This is called a dominant strategy. A dominant strategy is a strategy that always leads to the best payoff for a player, no matter what the other players do. A rational player will always play his dominant strategy. In this game, Alan’s dominant strategy is to confess.
Does Barry also have a dominant strategy? If Barry thinks Alan will confess, he should confess to reduce his sentence to six years from ten years. These options are in the first column under Alan confesses. Six has been underlined because it is Barry's best decision. Barry should also confess if he thinks Alan will deny because that would reduce his sentence to only one year. One has been underlined in green in the second column. Therefore, confessing is also Barry’s dominant strategy. Using Table 2, we conclude that both criminals will always confess to the crime no matter what they believe their partner will do and each spends six years in prison. Economists refer to this as a Nash equilibrium. A Nash equilibrium outcome is an expected outcome when no player can change his or her strategy for personal gain – assuming each player’s decision remains unchanged after learning the other players’ decisions. The Nash equilibrium is circled in Table 2.
Table 2
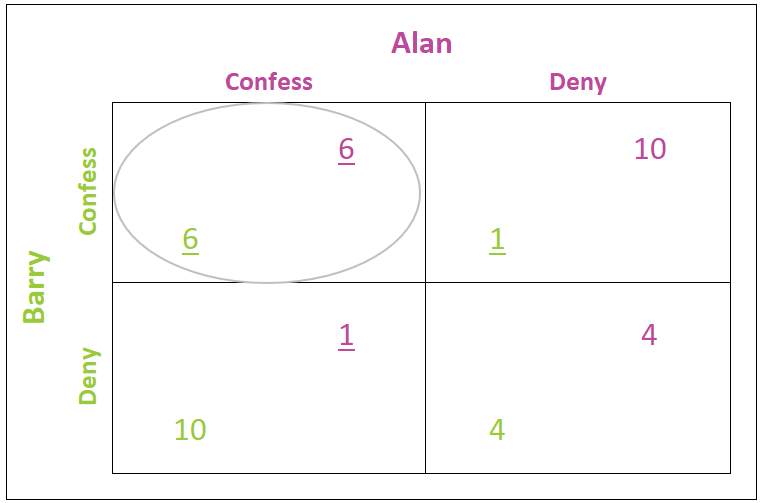
Why isn’t the most likely outcome where the criminals only spend four years in prison? After all, Alan and Barry would prefer being incarcerated for four years to serving six years. It is helpful to remember that both are acting independently. They do not know what the other person will do, and so they both act in their own best interest. If either player thinks the other will deny committing the crime, the player should confess to committing the crime and pass the blame onto the player who denied it. In that case, the person who confessed only spends one year in prison, and the person who denies spends ten years in prison! It is never the best idea to deny, even if one prisoner believes the other convict will also deny. The prisoner’s dilemma demonstrates how without cooperation the best outcome can be hard to reach even when all the players behave rationally.
Simultaneous games have been applied in military strategies, business decisions, politics, and many more scenarios when decisions are made at the same time, and one person’s decision influences the payoff for the other party.
Dig Deeper With These Free Lessons:
Game Theory
Market Structures Part II – Monopolistic Competition and Oligopoly
Market Structures Part I – Perfect Competition and Monopoly


